
So we can reduce the asymptotic complexity in log log n once and the memory consumption up to O(n½+o(1)), as in the Sieve of Eratosthenes using wheel factorization and segmentation. The author's optimized implementation in C is presented in the form of primegen, and a simplified version is in Wikipedia. It is clear from the description that the complexity of the Sieve of Atkin is proportional to n, rather than n log log n as in the algorithm of Eratosthenes. After computing the numbers of cells of the form 6k ± 1, containing odd numbers, they are prime numbers or divided into squares of primes.Īs a final step, we go sequentially through supposedly prime numbers and cross out multiples of their squares. Now, for each pair (x, y) where are incremented values in the cells S, S, and if x > y, then in S as well.
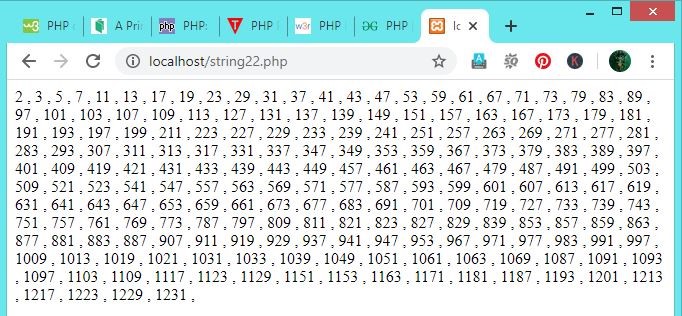
In order to initialize the algorithm fill the sieve S with zeros. The elementary number theory implies that all prime numbers more than 3 have the form 12k +1 (case 1), 12k +5 (again 1), 12k +7 (case 2) or 12k +11 (case 3). Let us write the algorithm of Eratosthenes in PHP.

How to find list of prime numbers how to#
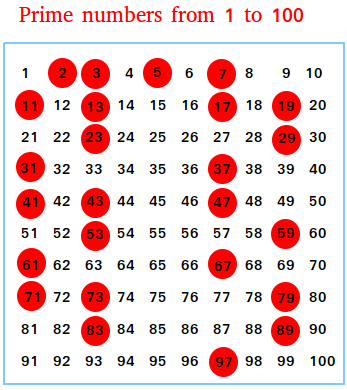
In is being discussed how to implement correctly the Sieve of Eratosthenes in Haskell using the technique of lazy crossings out. OCaml) allows that it is worth to break the standard specifications and create an alterable array. In general, the Sieve of Eratosthenes is difficult to implement effectively in the functional paradigm of invariant variables. However, the constructing complexity of differential sets is proportional to the size of the larger of them, so the result is O(n3/2-ε) operations. (n: Int) => (2 to n) |> (r => r.foldLeft(r.toSet)((ps, x) => if (ps(x)) ps - (x * x to n by x) else ps)) in Scala, it is near the Eratosthenes algorithm, because it avoids checking for divisibility. As a result the algorithm increases at least up to (this is the number of filtrations) that multiplied by (the minimum number of elements in the filtering set), where is the number of primes that does not exceed n, i.e. In Haskell) cause element wise checking divisibility. go over the possible divisors from 2 to sqrt (n) Thus, if we know how to factorize numbers then we can and check the numbers for simplicity. Numbers that have a greater number of divisors are called composite numbers. The number can be called a prime if it has exactly two distinct divisors: figure one and itself.


 0 kommentar(er)
0 kommentar(er)
